二叉树平衡

二叉平衡树（Balanced Binary Tree），又称为AVL树，是一种自平衡的二叉搜索树。在二叉平衡树中，任何节点的两个子树的高度最大差别不超过1，这样既保证了快速查找的时间复杂度（O(log n)），也避免了树的高度退化为链表。

平衡二叉树

平衡二叉树（Balanced Binary Search Tree, BBST）是指满足某种平衡条件的二叉搜索树，例如AVL树、红黑树等。这些树的平衡性保证了它们在插入和删除操作后的性能不会急剧下降。

平衡二叉树的调整

当进行插入或删除操作导致树失去平衡时，需要通过旋转来重新平衡树。常见的旋转有四种：左旋、右旋、左-右旋和右-左旋。

示例代码

定义一个树节点类，包含键值、左右子节点和高度属性

class TreeNode {
  constructor(key) {
      this.key = key; // 键值
      this.left = null; // 左子节点
      this.right = null; // 右子节点
      this.height = 1; // 初始高度设为1
  }
}

定义一个AVL树类，用于管理树结构

class AVLTree {
  constructor() {
      this.root = null; // 初始化树的根节点为空
  }

  // 获取节点的高度
  getHeight(node) {
      if (node === null) return 0; // 空节点高度为0
      return node.height;
  }

  // 计算节点的平衡因子
  getBalanceFactor(node) {
      if (node === null) return 0;
      return this.getHeight(node.left) - this.getHeight(node.right);
  }

  // 右旋操作，用于调整树的平衡
  rightRotate(y) {
      let x = y.left; // 获取y的左子节点
      let T2 = x.right; // 获取x的右子节点

      x.right = y; // 将y设置为x的右子节点
      y.left = T2; // 将T2设置为y的左子节点

      // 更新x和y的高度
      y.height = Math.max(this.getHeight(y.left), this.getHeight(y.right)) + 1;
      x.height = Math.max(this.getHeight(x.left), this.getHeight(x.right)) + 1;

      return x; // 返回新的根节点
  }

  // 左旋操作，与右旋类似
  leftRotate(x) {
      let y = x.right;
      let T2 = y.left;

      y.left = x;
      x.right = T2;

      x.height = Math.max(this.getHeight(x.left), this.getHeight(x.right)) + 1;
      y.height = Math.max(this.getHeight(y.left), this.getHeight(y.right)) + 1;

      return y;
  }

  // 插入新键值到树中
  insert(key) {
      this.root = this.insertNode(this.root, key);
  }

  // 递归地插入键值到树中，并调整树结构
  insertNode(node, key) {
      if (node === null) return new TreeNode(key); // 如果节点为空，则创建新节点并返回

      if (key < node.key) { // 插入左边
          node.left = this.insertNode(node.left, key);
      } else if (key > node.key) { // 插入右边
          node.right = this.insertNode(node.right, key);
      } else {
          return node; // 不允许插入重复键
      }

      // 更新节点的高度
      node.height = 1 + Math.max(this.getHeight(node.left), this.getHeight(node.right));

      // 获取平衡因子
      let balance = this.getBalanceFactor(node);

      // 根据平衡因子进行旋转调整
      // 左左情况
      if (balance > 1 && key < node.left.key) {
          return this.rightRotate(node);
      }
      // 右右情况
      if (balance < -1 && key > node.right.key) {
          return this.leftRotate(node);
      }
      // 左右情况
      if (balance > 1 && key > node.left.key) {
          node.left = this.leftRotate(node.left);
          return this.rightRotate(node);
      }
      // 右左情况
      if (balance < -1 && key < node.right.key) {
          node.right = this.rightRotate(node.right);
          return this.leftRotate(node);
      }

      return node; // 返回平衡后的节点
  }
}

创建并使用AVL树实例

let avlTree = new AVLTree();
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);

console.log(avlTree);

上述结果的数据结构

AVLTree
{
    root: {
        key: 20,
        left: {
            key: 10,
            left: null,
            right: null,
            height: 1
        },
        right: {
            key: 40,
            left: {
                key: 30,
                left: null,
                right: null,
                height: 1
            },
            right: {
                key: 50,
                left: null,
                right: null,
                height: 1
            },
            height: 2
        },
        height: 3
    }
}

数据结构可视化

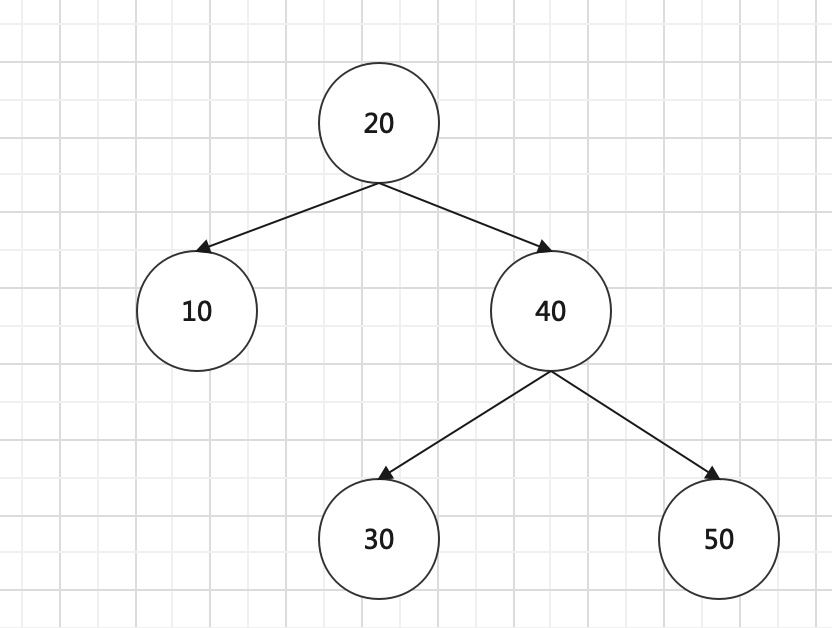
总结

总结

• 二叉平衡树 是一种自平衡的二叉搜索树，能够保证在插入和删除操作后树的结构保持相对平衡。
• 平衡二叉树 概念更广，包括所有满足特定平衡条件的二叉搜索树。
• 平衡二叉树的调整 是通过旋转操作来维护树的平衡，确保插入和删除操作后的时间复杂度仍为O(log n)。
• AVL树 实现了严格的平衡条件，每一步插入或删除后都需要进行调整以保持平衡。