二叉搜索树

静态查账与动态查找 针对动态查找，数据如何组织

名称（别称）

二叉搜索树（BST, Binary Search Tree）,也称二叉排序树或二叉查找树；

二叉搜索树特征

• 一棵二叉树，可以为空；
• 如果不为空，满足以下性质：:
  1. 非空左子树的所有键值小于其根结点的键值。
  2. 非空右子树的所有键值大于其根结点的键值。
  3. 左、右子树都是二叉搜索树。

错误示例

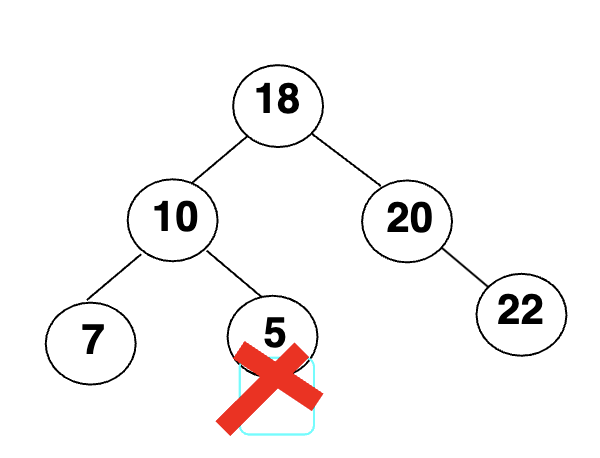
正确示例

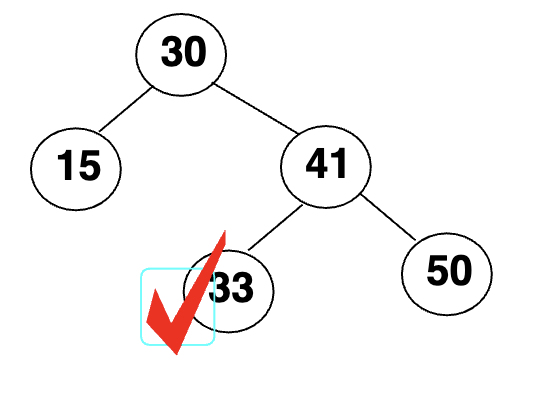
正确示例

二叉搜索树操作的特别函数：

• 💡Position Find( ElementType X, BinTree BST )：从二叉搜索树BST中查找元素X，返回其所在结点的地址；
• 💡Position FindMin( BinTree BST )：从二叉搜索树BST中查找并返回最小元素所在结点的地址；
• 💡Position FindMax( BinTree BST ) ：从二叉搜索树BST中查找并返回最大元素所在结点的地址。
• 💡BinTree Insert( ElementType X, BinTree BST )
• 💡BinTree Delete( ElementType X, BinTree BST )

二叉搜索树的查找操作Find

• 查找从根结点开始，如果树为空，返回NULL
• 若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
  • 若X小于根结点键值，只需在左子树中继续搜索；
  • 如果X大于根结点的键值，在右子树中进行继续搜索；
  • 若两者比较结果是相等，搜索完成，返回指向此结点的指针。

// 递归的形式
function findNode(X, BST) {
    if (!BST) return null; // 查找失败

    if (X > BST.data) {
        return findNode(X, BST.right); // 在右子树中继续查找
    } else if (X < BST.data) {
        return findNode(X, BST.left); // 在左子树中继续查找
    } else { // X === BST.data
        return BST; // 查找成功，返回结点的地址
    }
}

由于非递归函数的执行效率高，可将“尾递归”函数改为迭代函数

function findNode(X, BST) {
  while (BST) {
    if (X > BST.data) {
      BST = BST.right; // 向右子树中移动，继续查找
    } else if (X < BST.data) {
      BST = BST.left; // 向左子树中移动，继续查找
    } else { // X === BST.data
      return BST; // 查找成功，返回结点的地址
    }
  }
  return null
}

查找的效率决定于树的高度

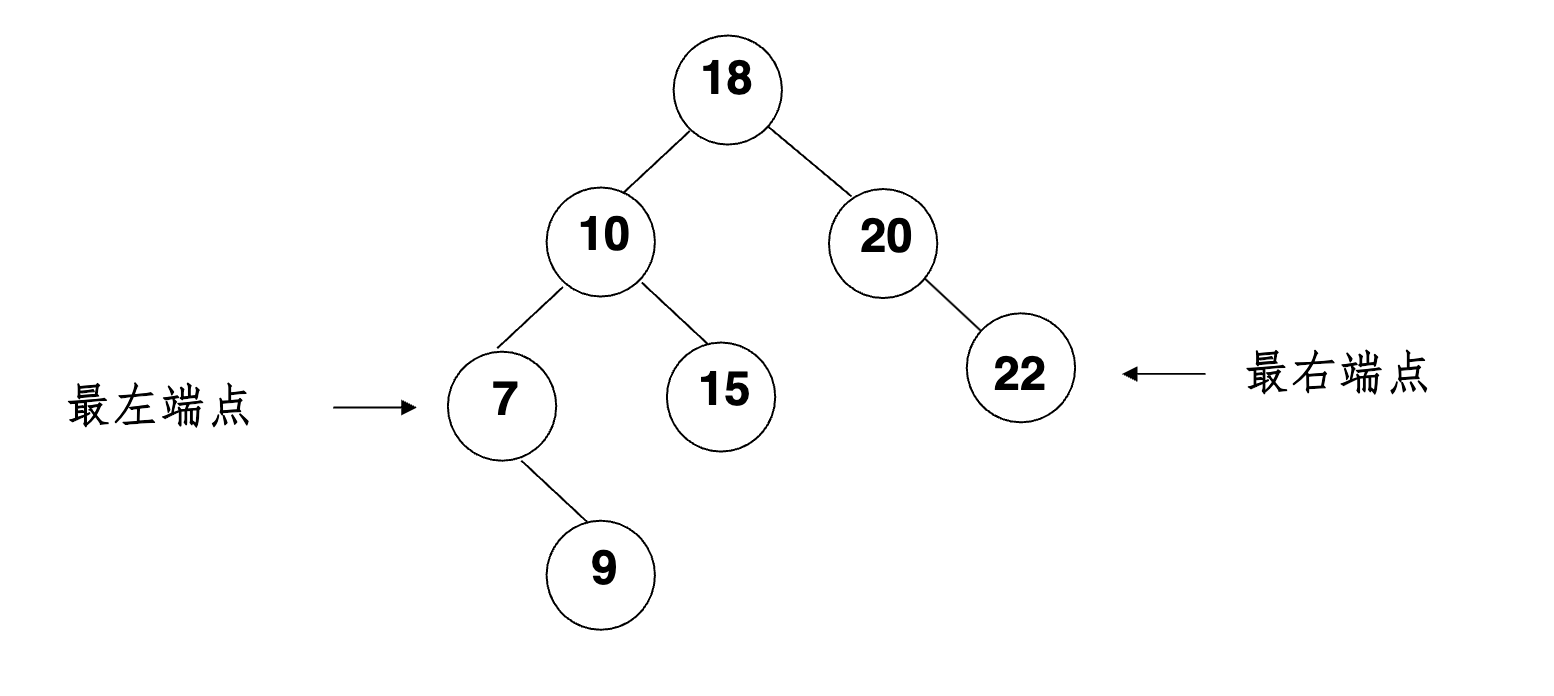
找最大和最小元素

• 最大元素一定是在树的最右分枝的端结点上
• 最小元素一定是在树的最左分枝的端结点上

// 查找最小元素的递归函数
function findMin(BST) {
  if (!BST) {
    return null, // /*空的二叉搜索树，返回null*/
  } else if (!BST.left) {
    return BST; //找到最左叶结点并返回
  } else {
    return findMin(BST.left)
  }
}

// 查找最大元素的迭代函数
function findMin(BST) {
  if (BST) {
    while (BST.right) {
      BST = BST.right; // 沿右分支继续查找，直到最右叶结点
    }
  }
  return BST;
}

二叉搜索树的插入

〖分析〗关键是要找到元素应该插入的位置，可以采用与Find类似的方法

• 在下面树上插入35

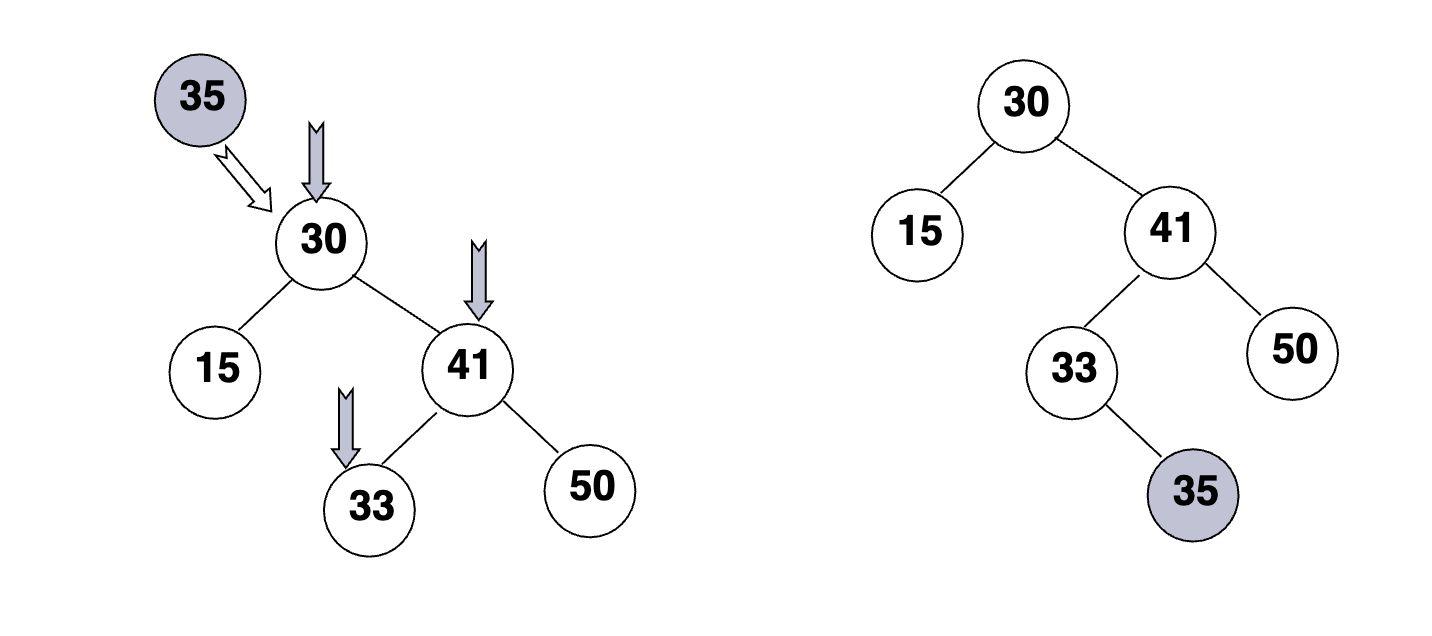
二叉搜索树的插入算法

function insert(X, BST) {
    if (!BST) { // 若原树为空，生成并返回一个结点的二叉搜索树
        BST = { data: X, left: null, right: null };
    } else { // 开始找要插入元素的位置
        if (X < BST.data) { // 递归插入左子树
            BST.left = insert(X, BST.left);
        } else if (X > BST.data) { // 递归插入右子树
            BST.right = insert(X, BST.right);
        } // else X已经存在，什么都不做
    }
    return BST;
}

二叉搜索树的删除

考虑三种情况

1. 要删除的是叶节点：直接删除，并再修改其父节点指针 ---置为null;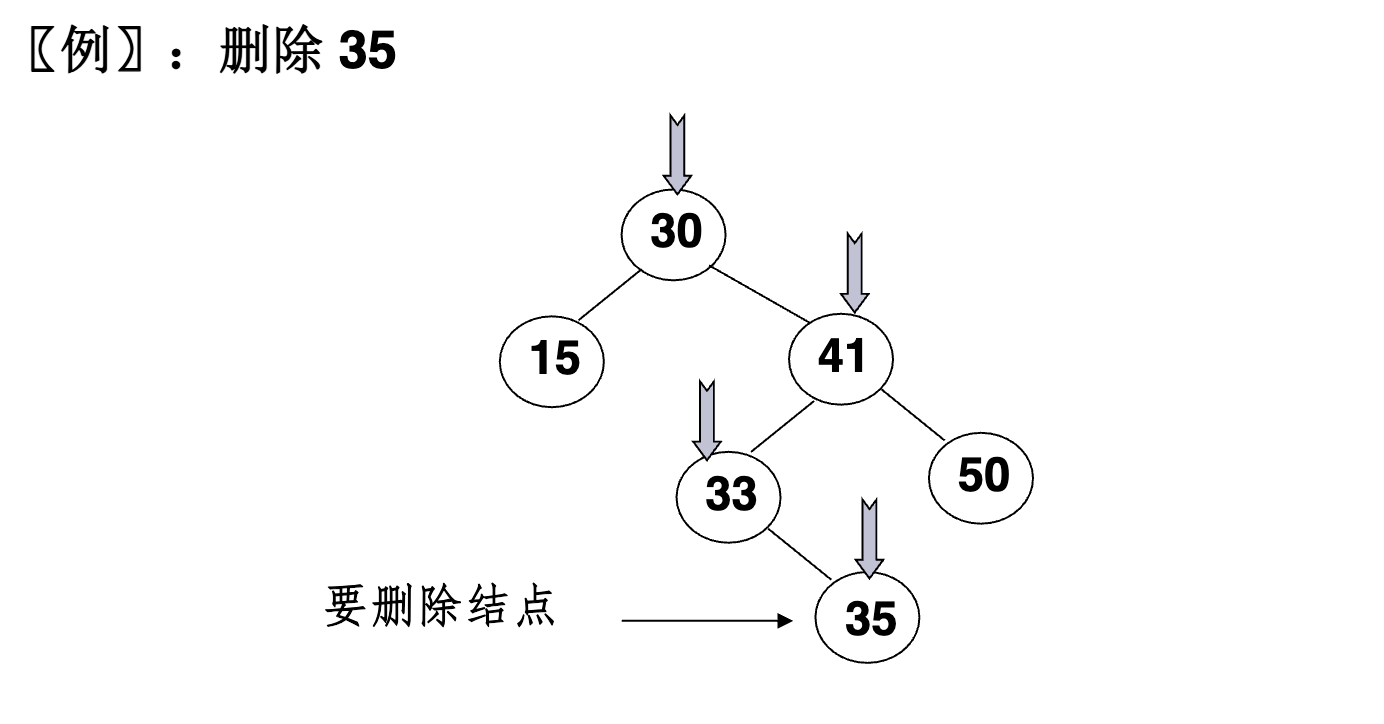
2. 要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点;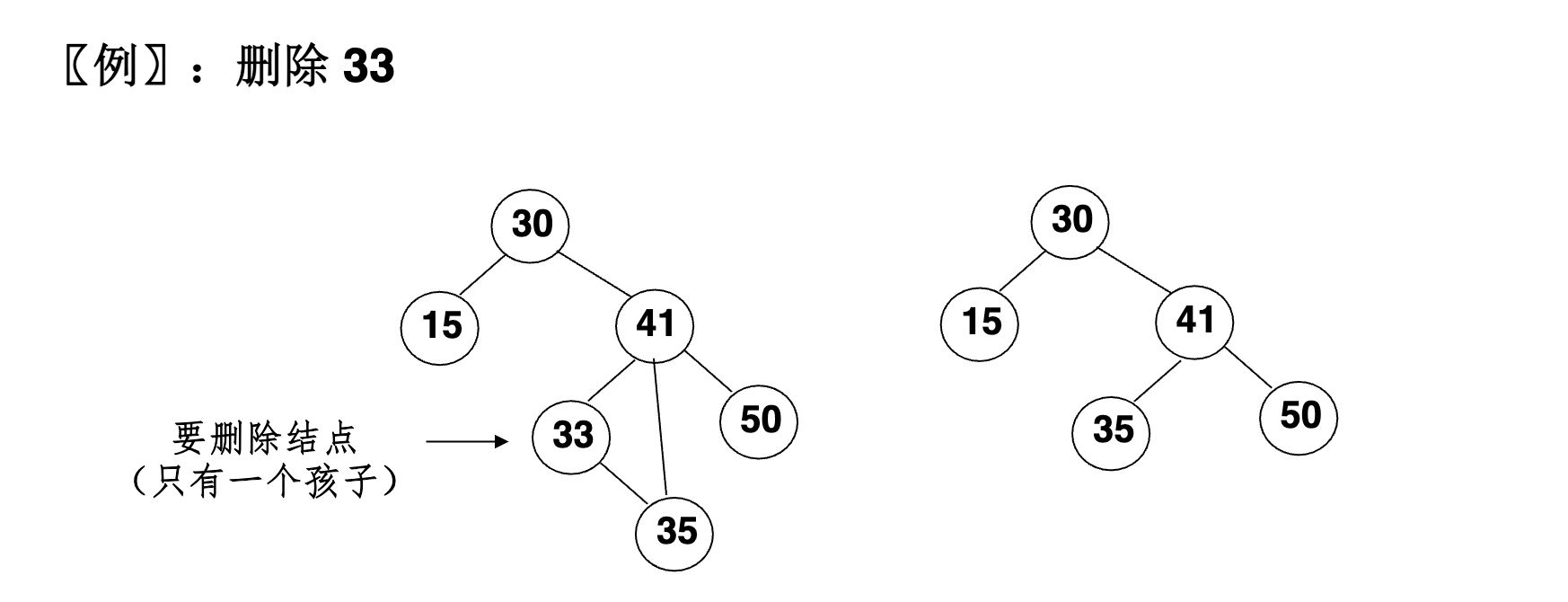
3. 要删除的结点有左、右两棵子树：用另一结点替代被删除结点：右子树的最小元素 或者 左子树的最大元素

二叉搜索树的删除实现

function deleteNode(X, BST) {
    let tmp;

    if (!BST) console.log("要删除的元素未找到");
    else if (X < BST.data) {
        BST.left = deleteNode(X, BST.left); // 左子树递归删除
    } else if (X > BST.data) {
        BST.right = deleteNode(X, BST.right); // 右子树递归删除
    } else { // 找到要删除的结点
        if (BST.left && BST.right) { // 被删除结点有左右两个子结点
            tmp = findMin(BST.right); // 在右子树中找最小的元素填充删除结点
            BST.data = tmp.data;
            BST.right = deleteNode(BST.data, BST.right); // 在删除结点的右子树中删除最小元素
        } else { // 被删除结点有一个或无子结点
            tmp = BST;
            if (!BST.left) { // 有右孩子或无子结点
                BST = BST.right;
            } else if (!BST.right) { // 有左孩子或无子结点
                BST = BST.left;
            }
            free(tmp); // 释放被删除结点的空间
        }
    }
    return BST;
}

function findMin(BST) {
    while (BST.left) {
        BST = BST.left;
    }
    return BST;
}